Chen CVPR’21 SimSiam (Exploring Simple Siamese Representation Learning)

Abstract

  • BYOLをシンプルにした

    • negative pair 使わない (BYOLと同じ)

    • momentum update 不要 (target networkを使わない)

    • batch size小さくてもOK

Linear Evaluation

../_images/simsiam_tab4.png

  • 100epoch以降は、BYOLには負けるが SimCLRとかには勝っている

transfer learning タスクでは強い

../_images/simsiam_tab5.png

Algorithm

準備

  • encoder (backbone + MLP) \(f\) と predictor (MLP) \(h\) を用意

以下繰り返し

  • \(x_1 = \text{aug}(x), x_2 = \text{aug}(x)\)

  • \(f(h(x_1))\) と \(\text{sg}(f(x_2))\) の距離を最小化　(sgは stop gradient)

    • 厳密には入力を入れ替えた \(f(h(x_2))\) と \(sg(f(x_1))\) の距離も最小化

../_images/simsiam_fig1.png

Empirical Study

(BYOLと同様negative pairを使っていないので、崩壊するように思えるが崩壊しない)

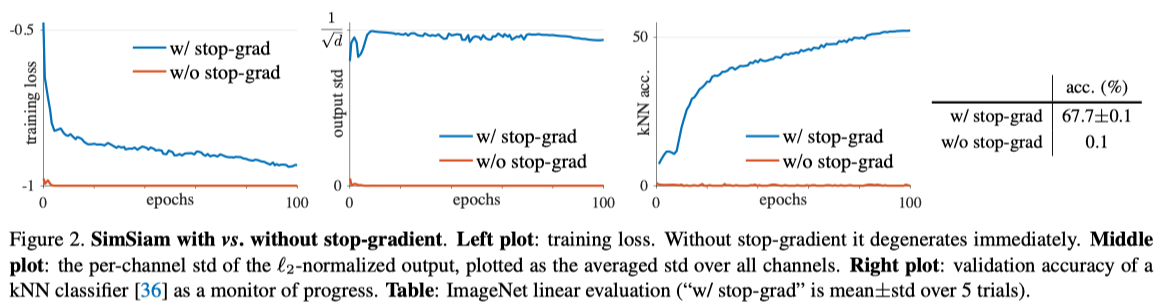
Fig2. Stop gradient しないと崩壊する

  • ロスはゼロになるが、出力の各次元の分散は0になり精度は上がらない

../_images/simsiam_fig2.png

Tab1. predictor (MLP) がないと崩壊する

../_images/simsiam_tab1.png

Tab2. batch size大きくしても精度上がらない

../_images/simsiam_tab2.png

Tab3. MLPにBatch Normalization いれないと精度が大きくさがる (一番うしろにBN入れると安定しない)

  • BYOLでも同じような結果になるらしい

../_images/simsiam_tab3.png

Hypothesis

(なぜ崩壊しないかの仮説ではない、SimSiamがどういう学習をしているのかの仮説)

以下のロス関数を考える

\begin{align} \mathcal{L}(\theta, \eta) = \mathbb{E}_{x, \mathcal{T}} \left[ \| \mathcal{F}_\theta(\mathcal{T}(x)) - \eta_x \|_2^2 \right] \end{align}

  • \(\mathcal{F}\) : ネットワーク (それのパラメータを \(\theta\) とする)

  • \(\eta\) : another set of variables (\(\eta\) のサイズは画像の数に比例する, \(\eta\) はネットワークの出力である必要はない)

そして、\(\mathcal{L}(\theta, \eta)\) を \(\theta, \eta\) に関して最小化することを考える. 交互最適化で最適化することを考える

\begin{align} \theta^t &\leftarrow \arg \min_{\theta} \mathcal{L}(\theta, \eta^{t-1}) \\ \eta^t &\leftarrow \arg \min_{\eta} \mathcal{L}(\theta^t, \eta) \end{align}

  • \(\theta\) に関してはSGDで解けばいい.

  • \(\eta\) に関する最適化は 各々の \(\eta_x\) について独立に解ける.　それでMSEなので、簡単に以下のように解ける.

(1)\[\eta^t_x \leftarrow \mathbb{E}_{\mathcal{T}} [\mathcal{F}_{\theta^t}(\mathcal{T}(x))]\]

SimSiamは (predictorを考えないと) この交互最適化の近似だとみなせる

  • (1) は \(\mathbb{E}_{\mathcal{T}}\) を 一回のaugmentation \(\mathcal{T'}\) によって近似すると以下になる

(2)\[\eta^t_x \leftarrow \mathcal{F}_{\theta^t}(\mathcal{T'}(x))\]

  • \(\eta\) についての最適化問題に (2) を代入すると、以下になって predictorを考えないと SimSiamの更新式みたいになる

(3)\[\theta^{t+1} \leftarrow \arg \min_{\theta} \mathbb{E}_{x, \mathcal{T}} \left[ \| \mathcal{F}_\theta(\mathcal{T}(x)) - \mathcal{F}_{\theta^t}(\mathcal{T'}(x)) \|_2^2 \right]\]

Predictor \(h\) のことを考える

  • \(h\)　は定義より, \(\mathbb{E}_{z}[\|h(z_1) - z_2\|_2^2]\) を最小化することが期待される (???)

  • この最適解は \(h(z_1) = \mathbb{E}_z[z_2] = \mathbb{E}_{\mathcal{T}}[f(\mathcal{T}(x))]\) を満たして、 (2) で (1) を近似したときのギャップを埋めてくれる (???)

わからないポイント: SimSiamは　\(h\) と \(f\) を一緒に最適化されるので、そうはならんのでは?

Proof of concept

実験的に証明すると言っている

  • (2) のように更新するのではなく、moving-averageする (momentum update)

    • つまり、 \(\eta_x^t \leftarrow m \eta_x^{t-1} + (1-m) \mathcal{F_{\theta^t}}(\mathcal{T}'(x))\)

  • こうすることによって、55%の精度が出せる

  • 表1(a)に示したように、predictorもmomving-averageもしないと崩壊する

  • 「この実験によって、predictor が \(\mathbb{E}_{\mathcal{T}}[\cdot]\) を関連していることが裏付けられた」と主張している

Methodology Comparisons

Q: PredictorやStop gradientをSimCLRに導入するとどうなるのか?

A: 精度は上がらない

../_images/simsiam_simclr.png