Movshovitz ICCV’17 No fuss distance metric learning using proxies¶
https://arxiv.org/abs/1703.07464
著者 (全員 GoogleResearch)
Yair Movshovitz-Attias
Alexander Toshev
Thomas K. Leung
Sergey Ioffe
Saurabh Singh
概要¶
\(\mathcal{P} = \{p_1, \ldots, p_L \}\), proxies (trainableな変数として、backpropの対象にして学習していく, L=クラス数)
\(d\) : 距離関数 (例: L2距離)
\begin{align}
L_{NCA}(x) := -
\log \cfrac{\exp(-d(x, p_y ))}
{\sum_{p \in \mathcal{P} \setminus \{p_y\} } \exp( -d(x, p))}
\end{align}
アイデア
サンプル同士でpairを作るのではなく、サンプルの分散表現と各クラスの代表の分散表現(Proxy)でペアを作って、ロスを計算する
Proxyはtrainableな変数で、Proxyにもbackpropして学習する
このアイデアは、どのロスにも応用可能

モチベーション
サンプル数=Nとして、Constructive lossだとペアの組み合わせは \(N^2\) で Triplet lossだと組み合わせは \(N^3\) で組み合わせが膨大になる
ミニバッチ数=bとすると、たとえばTriplet lossだと全組み合わせを学習するのに \(O((N/b)^3)\) iterationかかる (classification / reggressionなら \(O(N/b)\) iteration)
N = 1,000,000 で b=32だと \((N/b)^3 = 3.05 * 10^{13}\)
著者らの実験
Proxy NCAは収束が早いし、精度が良い

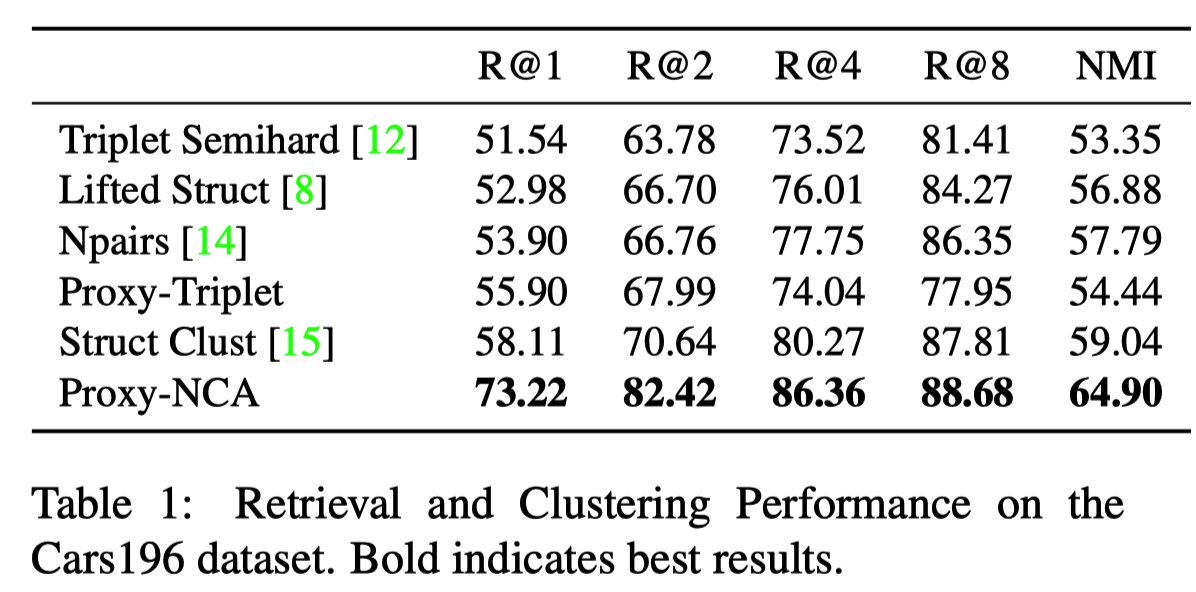
実験結果¶
CUB200

Cars196