Wang CVPR19 Multi-Similarity Loss with General Pair Weighting for Deep Metric Learning¶
https://arxiv.org/abs/1904.06627
著者 (全員 Malong Technologies )
Xun Wang
Xintong Han
Weiling Huang
Dengke Dong
Matthew R. Scott
概要¶
\(\alpha, \beta\) : スケーリングパラメータ(ハイパーパラメータ)
著者らの主張
relative similaritiesの性質は3つある ( \(w_{ij} := \partial L / \partial s(x_i, x_j)\) とする )
Simirarity-S
\(y_i \neq y_j\) で Sij (iとjの類似度)が大きくなった時, \(w_{ij}\) は大きなるべき
Simirarity-P
\(y_k = y_i \neq y_j\) で Sij < Sik のときより Sij > Sik のときのほうが \(w_{ij}\) 相対的に大きなるべき
Simirarity-N
\(y_k \neq y_i \neq y_j\) で Sij < Sik のときより Sij > Sik のときのほうが \(w_{ij}\) は相対的に大きなるべき
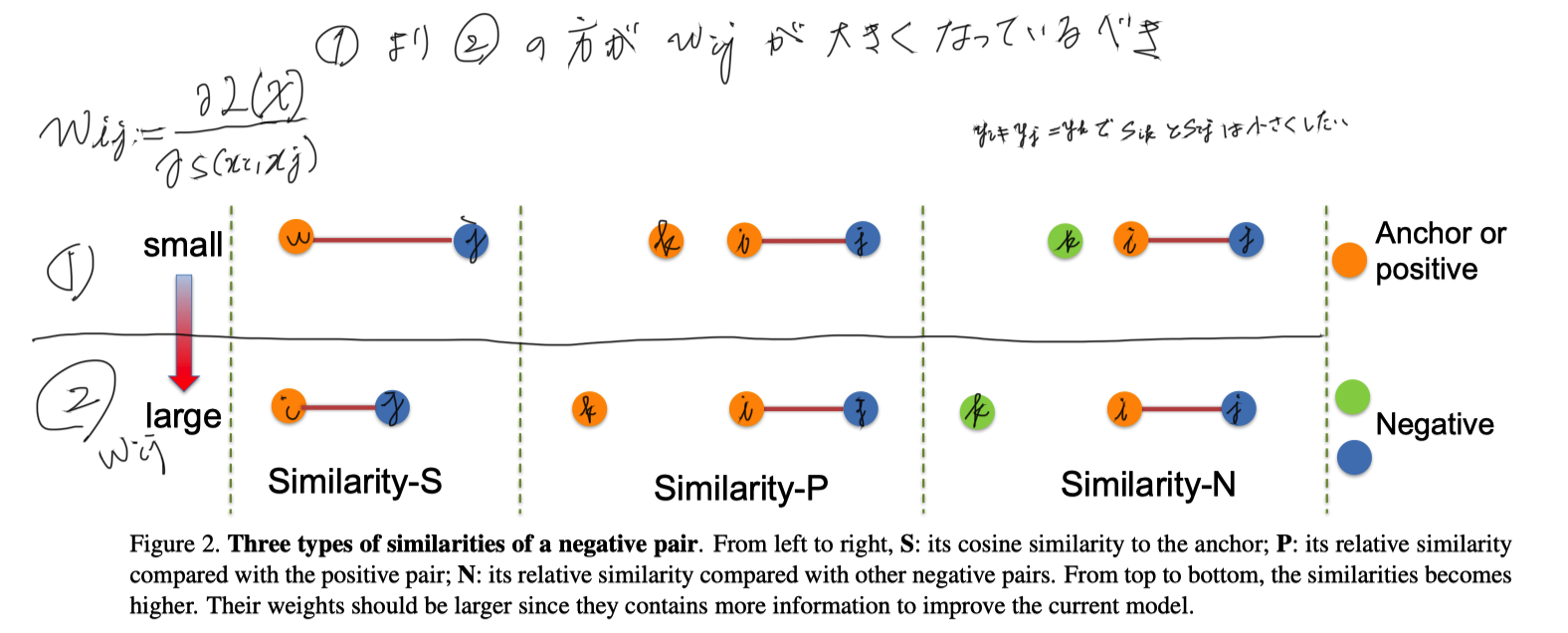
Metric learningのロスたちはそれらの性質を持っているのか?

Multi Similarty lossについて
\(w^{-}_{ij}\) はnegativeのほうの項をSijで微分したっぽい、論文中には定義はない
これで、Similarity-S, Simirality-Nは満たしていると言っている
Similarity-Pの方はどうなのか \(w^{+}_{ij}\) をみてもだめっぽい
Pair-miningをSimiratity-Pに基づいて行うからOKだと言っている
negative pairは、 \(S^{-}_{ij} > \min_{y_i = y_k} S_{ik} - \epsilon\) を満たすペアを学習に使う
positivef pairは \(S^{+}_{ij} < \max_{y_i \neq y_k} S_{ik} + \epsilon\) を満たすペアを学習に使う
実験¶
比較手法の精度をどうやって持ってきているのか書いてない、実験設定そろってない論文?
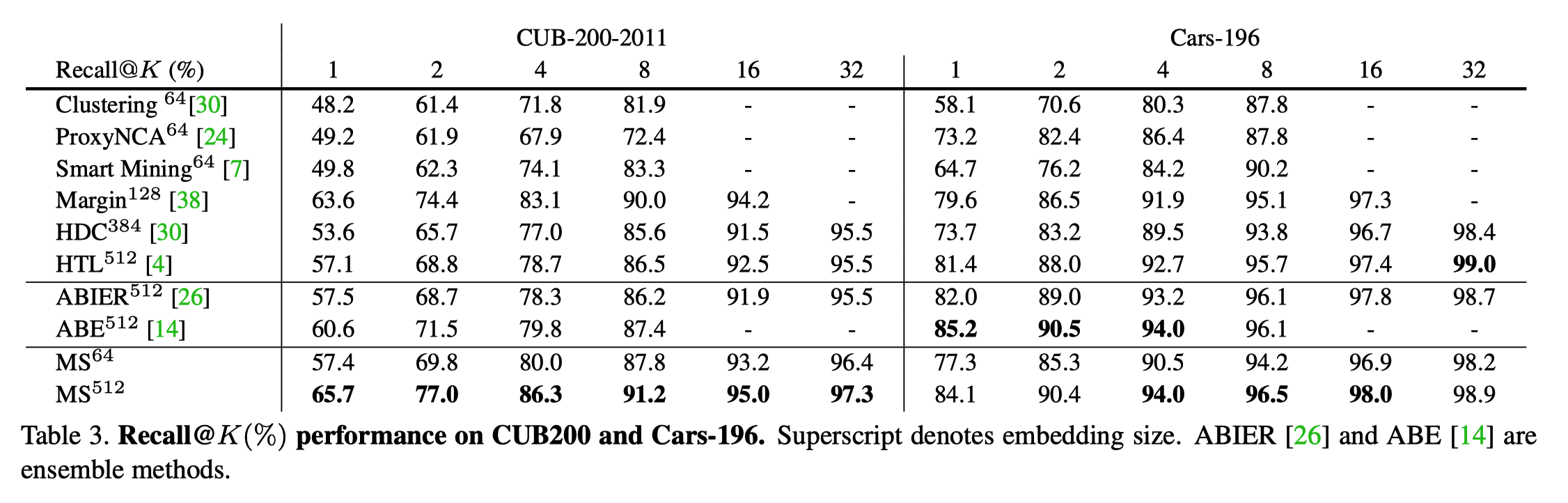
CUB-200 & Cars196
SOP
Wang CVPR’20 Cross-Batch Memory for Embedding Learning¶
https://arxiv.org/abs/1912.06798
著者 (全員 Malong Technologies )
Xun Wang
Haozhi Zhang
Weilin Huang
Matthew R. Scott
概要¶
アイデア
過去のminibatchで計算しておいた、embeddingを保持しておいてそれとのロスを計算させよう

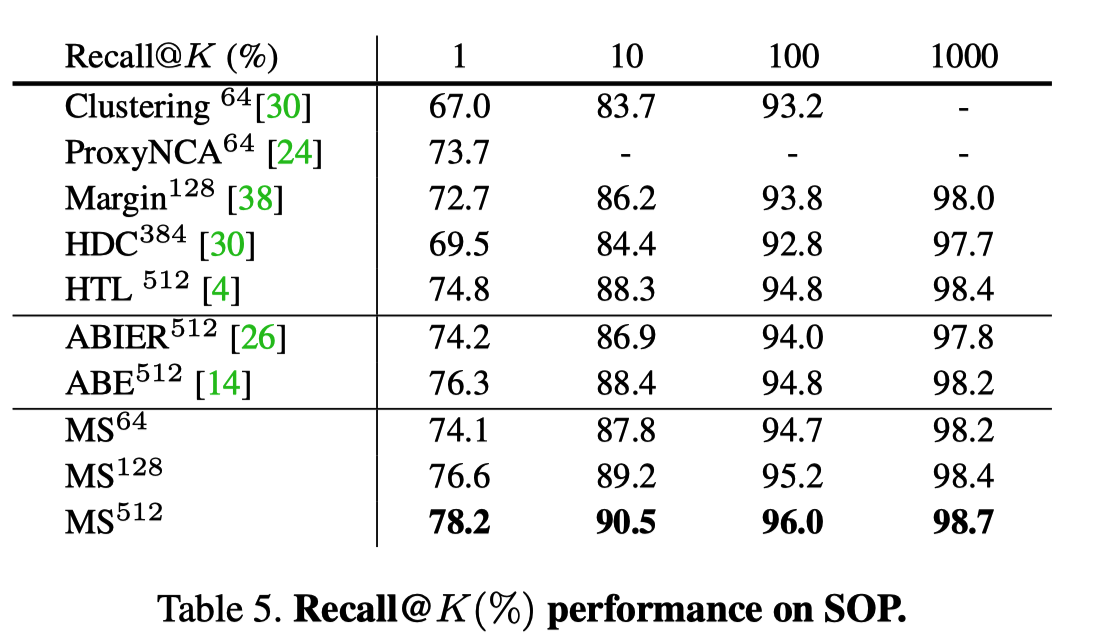
実験¶
contrastiveが一番いい・・・
MSの伸びが悪いのは外れ値の可能性がある極端な hard-negative の重みが高いためとい言っている