Zhuang SIGIR’20 Feature Transformation for Neural Ranking Models

https://research.google/pubs/pub49171/#:~:text=Feature%20transformation%20or%20normalization%20is,can%20benefit%20neural%20ranking%20models.

著者 (全員 Google Research)

  • Honglei Zhuang

  • Xuanhui Wang

  • Mike Bendersky

  • Marc Najork

概要

  • 木構造モデル: 数値データでのLTRで強い

    • 主に特徴のスケールの違いに影響されないの強い

  • ニューラルネットワークモデル: 画像やテキストデータを扱う上で非常に優れている

    • スケールが変化する特徴や歪んだ分布を持つ特徴に苦しむ

この論文の貢献

  • 特徴量の変換や正規化は基本的な手法だが、研究例が少なくそれがニューラルランキングモデルにどの程度の効果をもたらすかは不明

    • -> LTRタスクで実験的にその疑問に答える

  • 最適な性能をえるために、mixture transformationを提案する

    • 基本的な特徴量変換を線形結合し、その重みも学習可能な変数として学習してしまうという手法

    • -> 実験的にmixture transformationがNNランキングモデルの性能が大幅に向上することを示す

Basic Transformation

Gaussian transformation (z-score)

Notation

  • ひとつの標本データの特徴量はn個: \(x_i = (x_{i1}, \cdots, x_{in})\)

  • すべての標本データ: \(x_i \in \mathcal{X}\)

  • 特徴量kの標本平均: \(\hat{\mu_k}\), 標本標準偏差: \(\hat{s_k}\)

\begin{align} \sigma_{\text{Gauss},k} (x) := \frac{x - \hat{\mu_k} }{\hat{s_k}} \end{align}

CDF transformation

  • 各特徴量の累積分布関数(CDF)を推定し、その推定したCDFを用いて特徴量を変換する

\begin{align} \sigma_{\text{CDF},k} (x) := \frac{ \sum_{x_i \in \mathcal{X}} \mathbb{I}(x_{ik} < x) }{|\mathcal{X}|} \end{align}

Symmetric log1p transformation

  • log関数は0以下の値には適用できないし、0付近では値が吹っ飛んでしまうので

\begin{align} \sigma_{\text{Log1p},k} (x) := \text{sgn}(x) \cdot \log(1+|x|) \end{align}

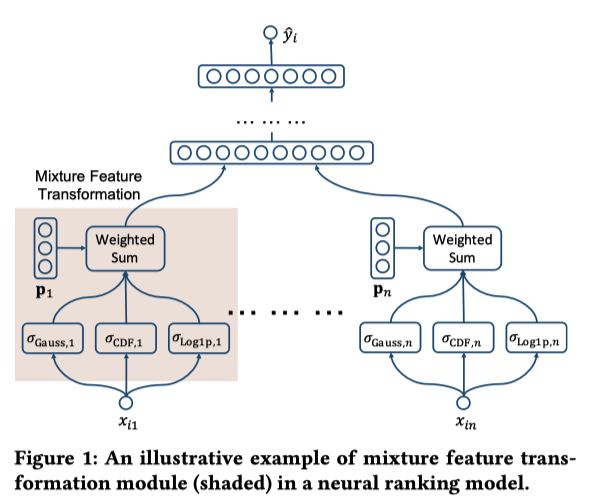
Mixture Transformation

  • m個の特徴量変換関数を用意する: \(\{ \sigma_{1,k}, \ldots, \sigma_{m,k} \}\)

\begin{align} \sigma_{\text{Mixture},k} (x) := \sum_{i=1}^{m} p_{i,k} \sigma_{i,k}(x) \end{align}

  • \(p_k := \text{softmax}(We_k)\) : m-dimensional weighting vector

    • \(e_k\) : d-dimensional embedding vector (学習する)

    • \(W: m \times d\) matrix (学習する)

  • 気持ち: ランキングモデルと jointlyに学習することで、各特徴量に最適な変換を自動的に決定できる

../_images/ltr_mt_f1.png

実験

Ranking Model

  • FC + ReLu 3層 (1024, 512, 256 units)

    • batch normalization layersのmometum = 0.4

    • dropout rate = 0.5

    • training batch size = 128

    • run 100,000 step

    • optimizer : Adagrad

    • learing rate: 0.5 for WEB30k, 0.1 for ISTELLA

  • loss : stochastic approximate NDCG@5

結果

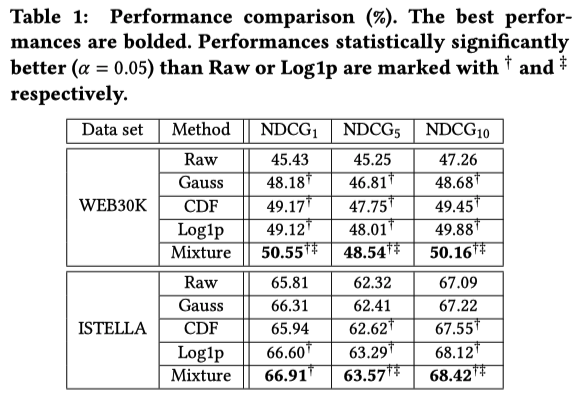
../_images/ltr_mt_t1.png

mixture weights の可視化 (WEB30k)

  • 縦軸: 特徴量

  • 横軸: 特徴量変換関数

  • 色: mixture weights

../_images/ltr_mt_f2.png